4654 2017-03-14 2020-06-25
前言:二叉树是一类重要的非线性数据结构,应用非常广泛,本篇将介绍几种常见的树。
一、二叉树
二叉树是一种树形结构,它的特点是每个节点至多只有两颗子树,并且,二叉树的子树有左右之分。
但单独的讨论二叉树意义不大,重点放在二叉树的某个特定子集,比如二叉查找树、AVL数、B树、红黑树、哈夫曼树等。
二、二叉查找树
1、定义
二叉查找树(Binary Search Tree),又称二叉搜索树,二叉排序树,它或者是一棵空树,或者是具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值。
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值。
- 任意节点的左、右子树也分别为二叉查找树。
- 没有键值相等的节点。
示例如图:
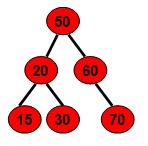
2、分析
二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低,为O(log n)。二叉查找树是基础性数据结构,用于构建更为抽象的数据结构,如集合、关联数组等。
二叉查找树的查找过程和二叉树类似,通常采取二叉链表作为二叉查找树的存储结构。中序遍历二叉查找树可得到一个关键字的有序序列,一个无序序列可以通过构造一棵二叉查找树变成一个有序序列,构造树的过程即为对无序序列进行查找的过程。每次插入的新的结点都是二叉查找树上新的叶子结点,在进行插入操作时,不必移动其它结点,只需改动某个结点的指针,由空变为非空即可。搜索、插入、删除的复杂度等于树高,期望O(log n),最坏O(n)(数列有序,树退化成线性表)。
虽然二叉查找树的最坏效率是O(n),但它支持动态查询,且有很多改进版的二叉查找树可以使树高为O(log n),如AVL树,红黑树等,故不失为一种好的动态查找方法。
3、代码实现
public class BinarySearchTree<E extends Comparable<? super E>> {
private BinaryNode<E> root;
public BinarySearchTree() {
root = null;
}
public void clearTree() {
root = null;
}
public boolean isEmpty() {
return root == null;
}
public void insert(E e) {
root = insert(e, root);
}
public boolean contains(E e) {
return contains(e, root);
}
public void remove(E e) {
root = remove(e, root);
}
public void inOrderTraverse() {
inOrderTraverse(root);
}
/**
* 先序遍历:根节点->左子树->右子树
*/
public void preOrderTraverse(BinaryNode<E> node) {
System.out.print(node.element + " ");
if (node.left != null) {
preOrderTraverse(node.left);
}
if (node.right != null) {
preOrderTraverse(node.right);
}
}
/**
* 中序遍历,输出有序序列:左子树->根节点->右子树
*/
public void inOrderTraverse(BinaryNode<E> node) {
if (node.left != null) {
inOrderTraverse(node.left);
}
System.out.print(node.element + " ");
if (node.right != null) {
inOrderTraverse(node.right);
}
}
/**
* 后序遍历:左子树->右子树->根节点
*/
public void postOrderTraverse(BinaryNode<E> node) {
if (node.left != null) {
postOrderTraverse(node.left);
}
if (node.right != null) {
postOrderTraverse(node.right);
}
System.out.print(node.element + " ");
}
public E findMin() {
if (isEmpty()) {
throw new RuntimeException("空树");
}
return findMin(root).element;
}
public E findMax() {
if (isEmpty()) {
throw new RuntimeException("空树");
}
return findMax(root).element;
}
private BinaryNode<E> insert(E e, BinaryNode<E> node) {
if (node == null) {
return new BinaryNode<>(e);
}
int compareResult = e.compareTo(node.element);
if (compareResult < 0) {
node.left = insert(e, node.left);
} else if (compareResult > 0) {
node.right = insert(e, node.right);
}
return node;
}
private boolean contains(E e, BinaryNode<E> node) {
if (node == null || e == null) {
return false;
}
int compareResult = e.compareTo(node.element);
// e小于,继续跟node的左子树比较
if (compareResult < 0) {
return contains(e, node.left);
} else if (compareResult > 0) {
return contains(e, node.right);
} else {
return true;
}
}
/**
* 参考下面的相关说明
*/
private BinaryNode<E> remove(E e, BinaryNode<E> node) {
if (node == null) {
return null;
}
int compareResult = e.compareTo(node.element);
if (compareResult < 0) {
node.left = remove(e, node.left);
} else if (compareResult > 0) {
node.right = remove(e, node.right);
} else if (node.left != null && node.right != null) {
// 把最小的节点与目标节点交换,再删除目标节点
node.element = findMin(node.right).element;
node.right = remove(node.element, node.right);
} else {
node = (node.left != null) ? node.left : node.right;
}
return node;
}
/**
* 递归形式
*/
private BinaryNode<E> findMin(BinaryNode<E> node) {
if (node == null) {
return null;
} else if (node.left == null) {
return node;
}
return findMin(node.left);
}
/**
* 非递归形式
*/
private BinaryNode<E> findMax(BinaryNode<E> node) {
if (node != null) {
while (node.right != null) {
node = node.right;
}
}
return node;
}
private static class BinaryNode<E> {
E element;
BinaryNode<E> left;
BinaryNode<E> right;
BinaryNode(E node) {
this(node, null, null);
}
BinaryNode(E node, BinaryNode<E> lt, BinaryNode<E> rt) {
element = node;
left = lt;
right = rt;
}
}
public static void main(String[] args) {
BinarySearchTree<Integer> bst = new BinarySearchTree<>();
bst.insert(6);
bst.insert(8);
bst.insert(9);
bst.insert(7);
bst.insert(3);
bst.insert(1);
bst.insert(2);
bst.insert(4);
bst.insert(0);
bst.insert(5);
bst.insert(4);
bst.insert(1);
bst.preOrderTraverse(bst.root);// 6 3 1 0 2 4 5 8 7 9
System.out.println();
bst.inOrderTraverse();// 0 1 2 3 4 5 6 7 8 9
System.out.println();
bst.postOrderTraverse(bst.root);// 0 2 1 5 4 3 7 9 8 6
System.out.println("\n" + bst.findMax());// 9
System.out.println(bst.findMin());// 0
System.out.println(bst.contains(1));// true
bst.remove(3);
bst.inOrderTraverse();// 0 1 2 4 5 6 7 8 9
// 测试通过
}
}
正如许多数据结构一样,最困难的操作是remove(删除)。一旦我们发现要被删除的节点,就需要考虑几种可能的情况。
如果节点是一片树叶,那么它可以被立即删除。如果节点有一个儿子,则该节点可以在其父节点调整自己的链以绕过该节点后被删除,图略。
复杂的情况是处理具有两个儿子的节点。一般的删除策略是用其右子树的最小数据(很容易找到)代替该节点的数据并递归地删除那个节点(现在它是空的)。因为右子树的最小节点不可能有左儿子,所以第二次remove要容易,如下图。
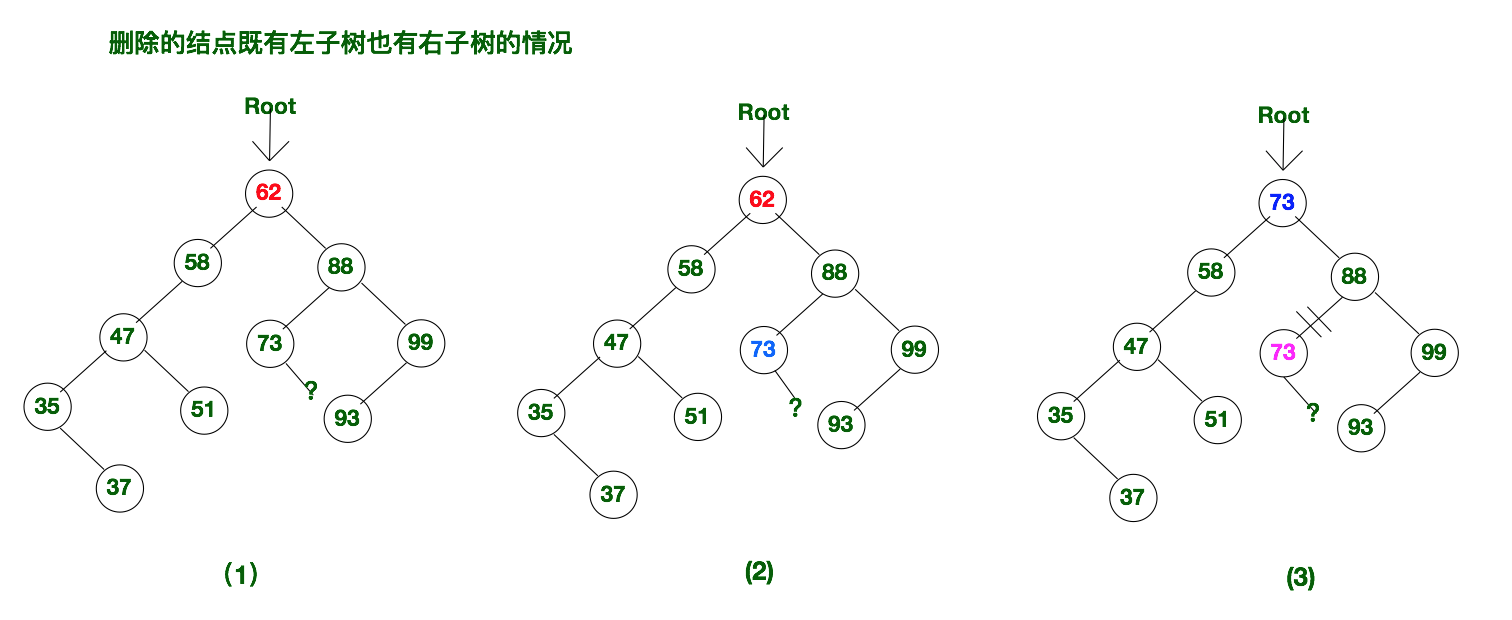
三、AVL树
1、定义
AVL树(Adelson-Velskii和Landis)是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差为1,所以它也被称为高度平衡树、平衡二叉树。
AVL树的查找、插入和删除在平均和最坏情况下的时间复杂度都是O(log n),增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。
由于平衡二叉树的平衡条件比较严格,故其维护的代价也较大(插入/删除操作后维持平衡需要),一般只适用于查找次数多、插入和删除次数少的情况。从实际出发,平衡条件较为宽松的红黑树是更好的选择,因为对其进行插入或删除操作付出的代价相对较小。当然,如果在应用场景中插入和删除操作并不频繁,只是对查找要求较高,那么平衡二叉树还是较优于红黑树。
2、操作
AVL树是平衡的二叉树,但当对其进行插入/删除操作时就很可能会破会这个平衡,此时我们可以通过旋转来维持平衡。
失衡的四种情况(把当前因失衡而必须重新平衡的结点叫做α)
- 对α的左儿子的左子树进行一次插入(左-左情况)
- 对α的左儿子的右子树进行一次插入(左-右情况)
- 对α的右儿子的左子树进行一次插入(右-左情况)
- 对α的右儿子的右子树进行一次插入(右-右情况)
其中情形1和4关于α点的镜像对称,而2和3关于α点的镜像对称。因此理论上只有两种情况,当然从编程的角度来看还是是四种情形。
第一种情况是插入发生在“外边”的情况(即左-左的情况或右-右的情况),该情况通过对树的一次单旋转而完成调整。第二种情况是插入发生在“内部”情况(即左-右的情况或右-左的情况),该情况可以通过稍微复杂的双旋转来处理。我们将会看到,这些都是对树的基本操作,它们多次用在一些平衡树算法中。
具体请参看AVL树(三)之 Java的实现,写得还不错。
- 单旋转
单旋转关键是找准k1和k2,过程如下图

代码实现如下
/**
* LL:左左对应的情况(左单旋转)。
*/
private AvlNode<T> leftLeftRotation(AvlNode<T> k2) {
AvlNode<T> k1;
k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
k1.height = Math.max(height(k1.left), k2.height) + 1;
return k1;
}

代码实现如下
/**
* RR:右右对应的情况(右单旋转)。
*/
private AvlNode<T> rightRightRotation(AvlNode<T> k1) {
AvlNode<T> k2;
k2 = k1.right;
k1.right = k2.left;
k2.left = k1;
k1.height = Math.max(height(k1.left), height(k1.right)) + 1;
k2.height = Math.max(height(k2.right), k1.height) + 1;
return k2;
},
- 双旋转
双旋转的关键是分清k1、k2、k3,过程如下图

代码实现如下
/**
* LR:左右对应的情况(左双旋转)。
*/
private AvlNode<T> leftRightRotation(AvlNode<T> k3) {
k3.left = rightRightRotation(k3.left);
return leftLeftRotation(k3);
}

代码实现如下
/**
* RL:右左对应的情况(右双旋转)。
*/
private AvlNode<T> rightLeftRotation(AvlNode<T> k1) {
k1.right = leftLeftRotation(k1.right);
return rightRightRotation(k1);
}
3、代码实现
完整代码如下(可直接运行)
public class AvlTree<T extends Comparable<? super T>> {
private boolean isTrace = true;
private static final int ALLOWED_IMBALANCE = 1;
private AvlNode<T> root;
public AvlNode<T> insert(T x) {
if (root == null) {
if (isTrace) {
System.out.println("节点" + x + "直接作为根节点 ");
}
return root = new AvlNode<>(x, null, null);
}
return root = insert(root, x);
}
/**
* 将T插入到AVL树中,并返回目标根节点
*/
private AvlNode<T> insert(AvlNode<T> tree, T x) {
if (tree == null) {
if (isTrace) {
System.out.println("返回新节点:" + x);
}
return new AvlNode<>(x, null, null);
}
int compareResult = x.compareTo(tree.key);
if (compareResult < 0) {
// x小于tree节点值,插入到tree的左子树
if (isTrace) {
System.out.println(x + "插入到" + tree + "的left");
}
tree.left = insert(tree.left, x);
} else if (compareResult > 0) {
// 将x插入到tree的右子树
if (isTrace) {
System.out.println(x + "插入到" + tree + "的right");
}
tree.right = insert(tree.right, x);
} else {
System.out.println("添加失败:不允许添加相同的节点!");
return tree;
}
return balance(tree);
}
private AvlNode<T> balance(AvlNode<T> tree) {
if (tree == null) {
return null;
}
boolean hasRotated = false;
if (height(tree.left) - height(tree.right) > ALLOWED_IMBALANCE) {
hasRotated = true;
System.out.print("节点" + tree + "的left高度比right高2 ");
if (height(tree.left.left) >= height(tree.left.right)) {
if (isTrace) {
System.out.println("节点" + tree + "需要左左单旋转,left" + tree.left + ",right" + tree.right);
}
tree = leftLeftRotation(tree);
} else {
if (isTrace) {
System.out.println("节点" + tree + "需要左右双旋转,left" + tree.left + ",right" + tree.right);
}
tree = leftRightRotation(tree);
}
} else if (height(tree.right) - height(tree.left) > ALLOWED_IMBALANCE) {
hasRotated = true;
System.out.print("节点" + tree + "的right高度比left高2 ");
if (height(tree.right.right) >= height(tree.right.left)) {
tree = rightRightRotation(tree);
} else {
tree = rightLeftRotation(tree);
}
}
if (isTrace) {
int newHeight = Math.max(height(tree.left), height(tree.right)) + 1;
System.out.println((hasRotated ? "旋转后" : "无需旋转") +"," + tree + "高度变为" + newHeight);
}
tree.height = Math.max(height(tree.left), height(tree.right)) + 1;
return tree;
}
public AvlNode<T> remove(T x) {
return remove(x, root);
}
private AvlNode<T> remove(T x, AvlNode<T> tree) {
if (tree == null) {
return null;
}
int compareResult = x.compareTo(tree.key);
// 待删除的节点在"tree的左子树"中
if (compareResult < 0) {
tree.left = remove(x, tree.left);
} else if (compareResult > 0) {
tree.right = remove(x, tree.right);
} else if (tree.left != null && tree.right != null) {
tree.key = findMin(tree.right).key;
tree.right = remove(tree.key, tree.right);
} else {
tree = (tree.left != null) ? tree.left : tree.right;
}
return balance(tree);
}
/**
* LL:左左对应的情况(左单旋转)。
*/
private AvlNode<T> leftLeftRotation(AvlNode<T> k2) {
AvlNode<T> k1;
k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
k1.height = Math.max(height(k1.left), k2.height) + 1;
return k1;
}
/**
* RR:右右对应的情况(右单旋转)。
*/
private AvlNode<T> rightRightRotation(AvlNode<T> k1) {
AvlNode<T> k2;
k2 = k1.right;
k1.right = k2.left;
k2.left = k1;
k1.height = Math.max(height(k1.left), height(k1.right)) + 1;
k2.height = Math.max(height(k2.right), k1.height) + 1;
return k2;
}
/**
* LR:左右对应的情况(左双旋转)。
*/
private AvlNode<T> leftRightRotation(AvlNode<T> k3) {
k3.left = rightRightRotation(k3.left);
return leftLeftRotation(k3);
}
/**
* RL:右左对应的情况(右双旋转)。
*/
private AvlNode<T> rightLeftRotation(AvlNode<T> k1) {
k1.right = leftLeftRotation(k1.right);
return rightRightRotation(k1);
}
public AvlNode<T> findMin() {
return findMin(root);
}
private AvlNode<T> findMin(AvlNode<T> node) {
if (node == null) {
return null;
} else if (node.left == null) {
return node;
}
return findMin(node.left);
}
private int height(AvlNode<T> tree) {
return tree == null ? -1 : tree.height;
}
public int height() {
return height(root);
}
private void print(AvlNode<T> tree, T key, int direction) {
if (tree != null) {
if (direction == 0) {
System.out.println(tree.key + " is root");
} else {
// tree是分支节点
String dire = direction == 1 ? "right" : "left";
System.out.println(tree.key + " is " + key + "'s " + dire + " child");
}
print(tree.left, tree.key, -1);
print(tree.right, tree.key, 1);
}
}
public void print() {
if (root != null) {
print(root, root.key, 0);
}
}
private static class AvlNode<T> {
T key;
int height;
AvlNode<T> left;
AvlNode<T> right;
public AvlNode(T key, AvlNode<T> left, AvlNode<T> right) {
this.key = key;
this.left = left;
this.right = right;
this.height = 0;
}
@Override
public String toString() {
return "[key=" + key + ",height=" + height + "]";
}
}
public static void main(String[] args) {
int[] arr = {3, 2, 1, 4, 5, 6, 7, 16, 15, 14, 13, 12, 11, 10, 8, 9};
AvlTree<Integer> tree = new AvlTree<>();
for (int i = 0; i < arr.length; i++) {
System.out.print("添加" + arr[i] + " ");
// 插入数据通过测试
tree.insert(arr[i]);
}
System.out.println("高度:" + tree.height());
System.out.println("最小值:" + tree.findMin());
System.out.println("树的详细信息:");
tree.print();
// 由于删除涉及的原理比较复杂,这里就跳过了,只给出代码实现
}
}
非Trace输出结果
高度:4
最小值:[key=1,height=0]
树的详细信息:
7 is root
4 is 7's left child
2 is 4's left child
1 is 2's left child
3 is 2's right child
6 is 4's right child
5 is 6's left child
13 is 7's right child
11 is 13's left child
9 is 11's left child
8 is 9's left child
10 is 9's right child
12 is 11's right child
15 is 13's right child
14 is 15's left child
16 is 15's right child
四、红黑树
1、定义
红黑树(red black tree)是具有下列着色性质的二叉查找树:
- 每一个节点或者着成红色,或者着成黑色。
- 根是黑色的。
- 如果一个节点是红色的,那么它的子节点必须是黑色的。
- 所有叶子都是黑色(叶子是NIL或NULL节点,即空引用)。
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

这些约束确保了红黑树的关键特性:从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。
因为每一个红黑树也是一个特定的二叉查找树,因此红黑树上的只读操作与普通二叉查找树上的只读操作相同。然而,在红黑树上进行插入操作和删除操作会导致不再匹配红黑树的性质。恢复红黑树的性质需要少量O(log n)的颜色变更(实际是非常快速的)和不超过三次树旋转(对于插入操作是两次)。虽然插入和删除很复杂,但操作时间仍可以保持为O(log n)次。
2、操作
知道一点即可,通过左右旋转和变色使修改后的树结构依旧保持红黑树结构即可。
五、哈夫曼树
1、定义
哈夫曼树(Huffman Tree),又称最优二叉树,具有以下性质:
- 从已给出的目标带权结点(单独的结点) 经过一种方式的组合形成一棵树,使树的带权路径长度最小。
- 带权值的结点都是叶子结点,权值越小的结点,其到根结点的路径越长。
其构建过程如图:

2、哈夫曼编码
在计算机数据处理中,霍夫曼编码使用变长编码表对源符号(如文件中的一个字母)进行编码,其中变长编码表是通过一种评估来源符号出现机率的方法得到的,出现机率高的字母使用较短的编码,反之出现机率低的则使用较长的编码,这便使编码之后的字符串的平均长度、期望值降低,从而达到无损压缩数据的目的。
例如,在英文中,e的出现机率最高,而z的出现概率则最低。当利用霍夫曼编码对一篇英文进行压缩时,e极有可能用一个比特来表示,而z则可能花去25个比特(不是26)。用普通的表示方法时,每个英文字母均占用一个字节,即8个比特。二者相比,e使用了一般编码的1/8的长度,z则使用了3倍多。倘若我们能实现对于英文中各个字母出现概率的较准确的估算,就可以大幅度提高无损压缩的比例。
3、代码实现
public class HuffmanTree<E> {
public static <E> TreeNode<E> createHuffman(List<TreeNode<E>> nodes) {
if (nodes == null) {
throw new NullPointerException();
}
Collections.sort(nodes);
while (nodes.size() > 1) {
//降序排序
Collections.sort(nodes);
int size = nodes.size();
TreeNode<E> bestMin = nodes.get(size - 1);
TreeNode<E> min = nodes.get(size - 2);
TreeNode<E> parent = new TreeNode<>(null, bestMin.weight + min.weight);
//默认左边小于右边
parent.setLeft(bestMin);
parent.setRight(min);
nodes.remove(bestMin);
nodes.remove(min);
nodes.add(parent);
}
return nodes.get(0);
}
/**
* 广度优先遍历
*/
public static<E> void breadthFirst(TreeNode<E> root) {
Queue<TreeNode<E>> queue = new LinkedList<>();
if (root != null) {
queue.offer(root);
}
while (!queue.isEmpty()) {
TreeNode<E> temp = queue.poll();
System.out.println(temp.toString());
if (temp.left != null) {
queue.offer(temp.left);
}
if (temp.right != null) {
queue.offer(temp.right);
}
}
}
public static class TreeNode<E> implements Comparable<TreeNode<E>> {
E element;
double weight;
TreeNode<E> left, right;
public TreeNode(E e, double weight) {
this.element = e;
this.weight = weight;
}
public TreeNode<E> getLeft() {
return left;
}
public void setLeft(TreeNode<E> left) {
this.left = left;
}
public TreeNode<E> getRight() {
return right;
}
public void setRight(TreeNode<E> right) {
this.right = right;
}
@Override
public int compareTo(TreeNode<E> e) {
//降序排列
if (this.weight < e.weight) {
return 1;
} else if (this.weight > e.weight) {
return -1;
}
return 0;
}
@Override
public String toString() {
return element + "-weight:" + weight;
}
}
public static void main(String[] args) {
TreeNode<String> a = new TreeNode<>("a", 7);
TreeNode<String> b = new TreeNode<>("b", 5);
TreeNode<String> c = new TreeNode<>("c", 2);
TreeNode<String> d = new TreeNode<>("d", 4);
List<TreeNode<String>> list = new ArrayList<>();
list.add(a);
list.add(b);
list.add(c);
list.add(d);
TreeNode<String> root = HuffmanTree.createHuffman(list);
HuffmanTree.breadthFirst(root);
//结果如下
//null-weight:18.0
//a-weight:7.0
//null-weight:11.0
//b-weight:5.0
//null-weight:6.0
//c-weight:2.0
//d-weight:4.0
}
}
有了哈夫曼树后,哈夫曼编码就一目了然了(约定左分支表示字符‘0’,右为‘1’),这里就不再实现了。
六、其他树
有待补充….
总访问次数: 89次, 一般般帅 创建于 2017-03-14, 最后更新于 2020-06-25
 欢迎关注微信公众号,第一时间掌握最新动态!
欢迎关注微信公众号,第一时间掌握最新动态!