3799 2017-03-28 2020-06-25
前言:图是一种较线性表和树更为复杂的数据结构,应用非常广泛。
一、图的存储结构
1、邻接矩阵
用两个数组分别存储数据元素(顶点)的信息和数据元素之间的关系(边或弧)的信息。实例如下:
- 无向图
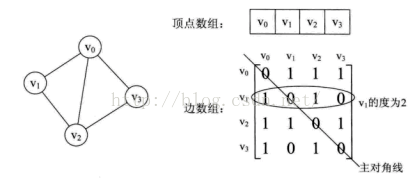
- 有向图
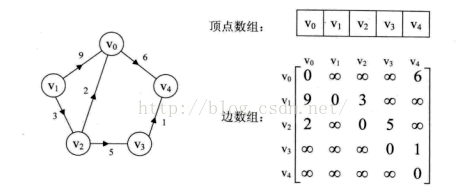
2、邻接表
邻接矩阵是一种不错的图存储结构,查询速度快,但耗空间。邻接表查询速度相对较慢,但相对的比较省空间。
邻接表的处理方法是这样的:
- 图中顶点用一个一维数组存储。
- 图中每个顶点Vi的所有邻接点用单链表来存储。
实例如下:
- 无向图

- 有向图
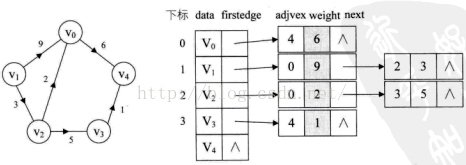
3、其他
其他的还有十字链表、邻多重表等,有待补充….
二、代码实现
1、顶点
public class Vertex<E> {
E element;
public Vertex(E e) {
this.element = e;
}
@Override
public String toString() {
return element.toString();
}
}
2、边
public class Edge implements Comparable<Edge> {
private Vertex from;
private Vertex to;
private int weight;
public Edge(Vertex from, Vertex to, int weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
public Vertex getFrom() {
return from;
}
public void setFrom(Vertex from) {
this.from = from;
}
public Vertex getTo() {
return to;
}
public void setTo(Vertex to) {
this.to = to;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
@Override
public int compareTo(Edge o) {
return this.weight - o.getWeight();
}
}
3、基本代码
public class Graph {
enum GraphType {
/**
* 有向图
*/
Digraph,
/**
* 无向图
*/
Undigraph;
}
private static final int MAX = Integer.MAX_VALUE;
private int[][] adjMatrix;
private boolean[] visited;
private Vertex[] vertices;
private Edge[] edges;
public Graph(int[][] arr) {
if (arr.length > 1 && arr[0].length == arr.length) {
this.adjMatrix = arr;
}
}
public Graph(Vertex[] vertices, Edge[] edges, GraphType type) {
this.vertices = vertices;
this.edges = new Edge[edges.length];
for (int i = 0; i < edges.length; i++) {
this.edges[i] = edges[i];
}
adjMatrix = new int[vertices.length][vertices.length];
for (int i = 0; i < vertices.length; i++) {
for (int j = 0; j < vertices.length; j++) {
adjMatrix[i][j] = MAX;
}
}
for (int i = 0; i < edges.length; i++) {
int fromIndex = -1, toIndex = -1;
for (int j = 0; j < vertices.length; j++) {
if (edges[i].getFrom() == vertices[j]) {
fromIndex = j;
}
if (edges[i].getTo() == vertices[j]) {
toIndex = j;
}
}
if (type == GraphType.Digraph) {
adjMatrix[fromIndex][toIndex] = edges[i].getWeight();
} else {
adjMatrix[fromIndex][toIndex] = edges[i].getWeight();
adjMatrix[toIndex][fromIndex] = edges[i].getWeight();
}
}
}
public Graph(Vertex[] vertices, Edge[] edges) {
this(vertices, edges, GraphType.Digraph);
}
public Graph(Vertex[] vertices, List edges) {
this(vertices, (Edge[]) edges.toArray(new Edge[edges.size()]));
}
}
4、遍历
/**
* 深度优先遍历
*/
public void depthFirstSearch() {
visited = new boolean[adjMatrix.length];
System.out.print("深度优先遍历: ");
for (int i = 0; i < adjMatrix.length; i++) {
if (!visited[i]) {
depthFirstSearch(i);
}
}
}
/**
* 广度优先遍历
*/
public void breadthFirstSearch() {
visited = new boolean[adjMatrix.length];
System.out.print("广度优先遍历: ");
Queue<Integer> queue = new LinkedList<>();
queue.offer(0);
while (!queue.isEmpty()) {
int index = queue.poll();
for (int i = index + 1; i < adjMatrix.length; i++) {
if (adjMatrix[index][i] != MAX && !visited[i]) {
queue.offer(i);
visited[i] = true;
}
}
System.out.print(vertices[index] + "(" + queue.size() + ") -> ");
}
}
private void depthFirstSearch(int startVertexIndex) {
visited[startVertexIndex] = true;
System.out.print(vertices[startVertexIndex] + " -> ");
for (int i = startVertexIndex + 1; i < adjMatrix.length; i++) {
if (adjMatrix[startVertexIndex][i] != MAX && !visited[i]) {
depthFirstSearch(i);
}
}
}
public void printGraph() {
for (int[] temp : adjMatrix) {
for (int i : temp) {
if (i == MAX) {
System.out.print(0 + " ");
} else {
System.out.print(i + " ");
}
}
System.out.println();
}
}
private void printArr(int[][] arr) {
for (int[] temp : arr) {
printArr(temp);
}
System.out.println();
}
private void printArr(int[] arr) {
for (int temp : arr) {
if (temp == MAX) {
System.out.print("max ");
} else {
System.out.print(temp + " ");
}
}
System.out.println();
}
三、最小生成树
在含有n个顶点的连通图中选择n-1条边,构成一棵极小连通子图,并使该连通子图中n-1条边上权值之和达到最小,则称其为连通网的最小生成树。
关于最小生成树,又称MST(Minimum Spanning Tree),有两个算法,分别是普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法。这里对算法思想进行大致讲解,并给出算法求解过程及代码实现,具体思想及原理还请读者自行翻阅相关书籍。
1、普里姆(Prim)
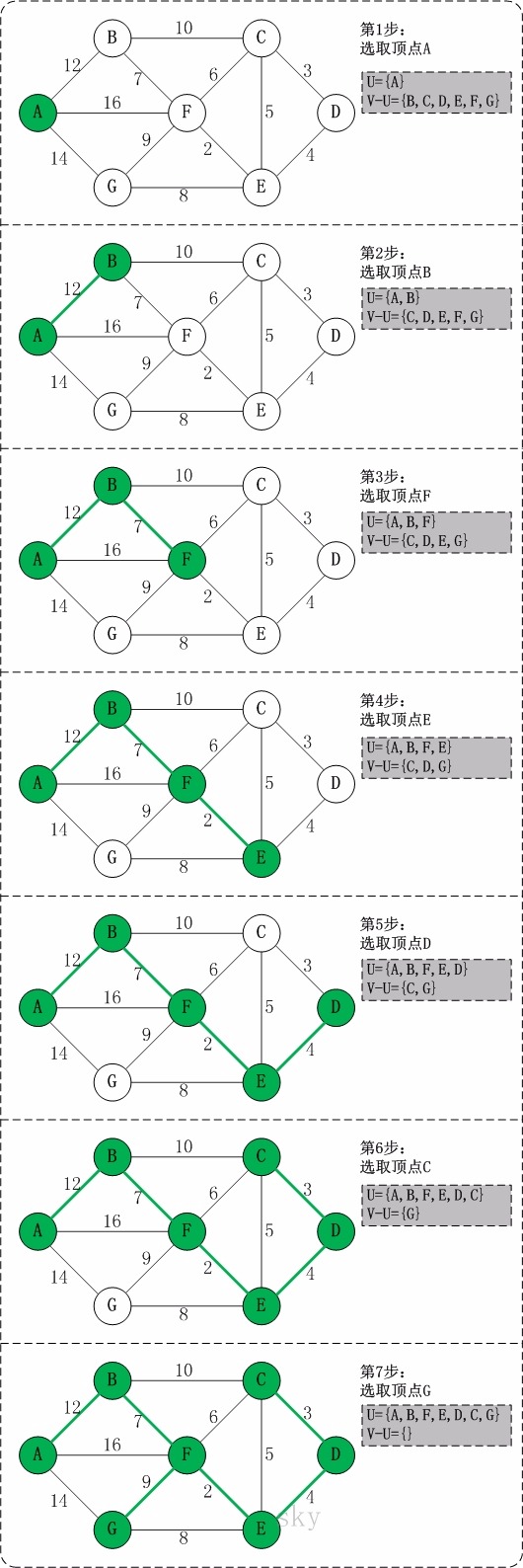
大致思想是:设图G顶点集合为U,首先任意选择图G中的一点作为起始点a,将该点加入集合V,再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小,此时将b点也加入集合V;以此类推,现在的集合V={a,b},再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小,此时将c点加入集合V,直至所有顶点全部被加入V,此时就构建出了一颗MST。因为有N个顶点,所以该MST就有N-1条边,每一次向集合V中加入一个点,就意味着找到一条MST的边。
算法求解过程如图:
public void prim() {
System.out.println("Prim算法:");
int[][] arr = adjMatrix;
//统计最小的权
int sum = 0;
//当前最小生成树所能到达的顶点的最小权数组
int[] costs = new int[arr.length];
//当前各个顶点对应的起点
int[] startPoint = new int[arr.length];
//初始化
for (int i = 1; i < arr.length; i++) {
//所有点的起点赋值为0
startPoint[i] = 0;
//以0为起点到达各个顶点的权值
costs[i] = arr[0][i];
}
//挑选剩余的8个顶点
for (int i = 1; i < arr.length; i++) {
//记录当前costs里面的最小权值是多少
int min = MAX;
//记录当前costs里面的最小权值对应的数组下标,即顶点
//(数组[顶点]=该顶点对应的起点)
int minIndex = 0;
//遍历costs
for (int j = 1; j < arr.length; j++) {
int temp = costs[j];
//costs[j]==0代表节点j已加入MST
if (temp != 0 && temp < min) {
min = temp;
minIndex = j;
}
}
sum += min;
//将已加入MST的对应的权值赋值为0
costs[minIndex] = 0;
System.out.println("最小生成树边有顶点 v" + (startPoint[minIndex] + 1) + "到顶点 v" + (minIndex + 1) + " ,权值为 " + min);
//选定了新的顶点到MST后,树到达各顶点的最小开销和起点将更新
//更新costs和startPoint
for (int k = 0; k < arr.length; k++) {
//用minIndex顶点到各个顶点的权值比较costs数组的值,若较小则替换,并更新起点为minIndex
int newCost = arr[minIndex][k];
if (newCost != MAX && newCost < costs[k]) {
costs[k] = newCost;
//更新K的起点为minIndex
startPoint[k] = minIndex;
}
}
}
System.out.println("该图最小生成树的权最小值为: " + sum + "\n");
}
2、克鲁斯卡尔(Kruskal)
克鲁斯卡尔算法的核心思想是:在带权连通图中,不断地在边集合中找到最小的边,如果该边满足得到最小生成树的条件,就将其构造,直到最后得到一颗最小生成树。
克鲁斯卡尔算法的执行步骤:
- 第一步:在带权连通图中,将边的权值排序;
- 第二步:判断是否需要选择这条边(此时图中的边已按权值从小到大排好序)。判断的依据是边的两个顶点是否已连通,如果连通则继续下一条;如果不连通,那么就选择使其连通。
- 第三步:循环第二步,直到图中所有的顶点都在同一个连通分量中,即得到最小生成树。
算法求解过程如图:
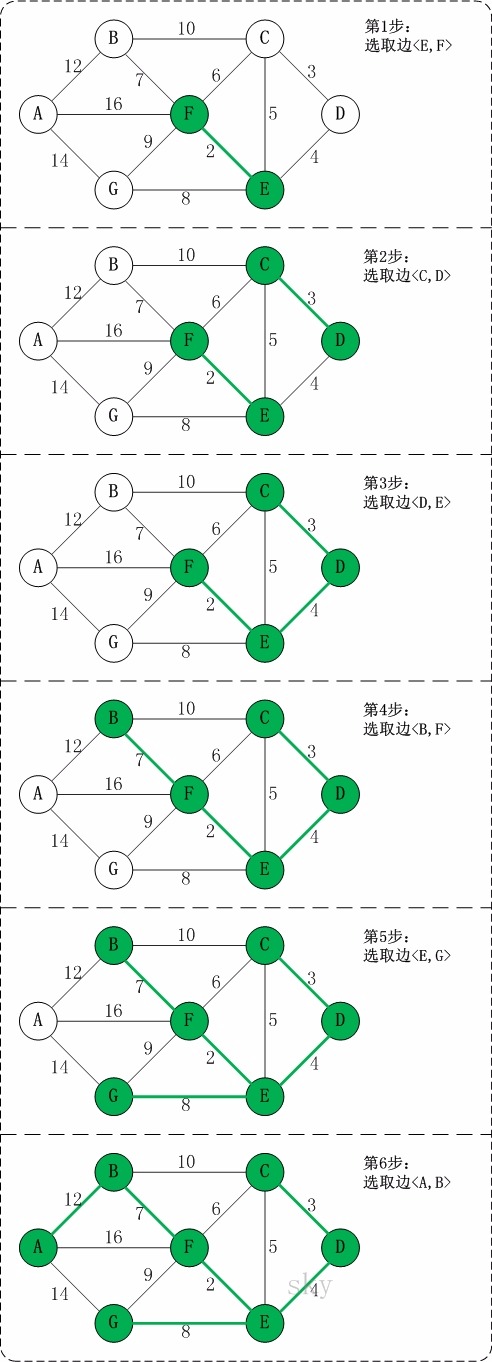
代码如下:
public void kruskal() {
System.out.println("Kruskal算法:");
Arrays.sort(edges);
/**
* 这个parent的作用很大,通过数组坐标和数组值,来判断是否是回路,读者自己走一遍就知道了
*/
int[] parent = new int[vertices.length];
int sum = 0;
for (int i = 0; i < edges.length; i++) {
Edge edge = edges[i];
int from = findVertex(edge.getFrom());
int to = findVertex(edge.getTo());
int m = find(from, parent);
int n = find(to, parent);
if (m != n) {
parent[m] = n;
System.out.println("最小生成树边有顶点 v" + (from + 1) + " 到定点 v" + (to + 1) + " 权值为 " + edge.getWeight());
sum += edge.getWeight();
}
}
System.out.println("该图最小生成树的权最小值为: " + sum + "\n");
}
private int findVertex(Vertex vertex) {
for (int i = 0; i < vertices.length; i++) {
if (vertex == vertices[i]) {
return i;
}
}
return -1;
}
private int find(int index, int[] parent) {
while (parent[index] > 0) {
index = parent[index];
}
return index;
}
四、最短路径
1、迪杰斯特拉(Dijkstra)
思想及原理略。
算法求解过程如图:

代码实现:
public void dijkstra(int[][] arr) {
System.out.println("Dijkstra算法:");
// 保存每个节点的前驱,即从哪个节点走到当前节点去,path[1]=0表示从节点0走到1去
int[] path = new int[arr.length];
// 到当前节点的最短开销 costs[5]=100表示当前最短路径到节点5的开销为100
int[] costs = new int[arr.length];
// 对于确定了最短路径的节点赋值为true,没确定的false
boolean[] isCompleted = new boolean[arr.length];
// 初始化节点0到各个节点的权值
for (int i = 0; i < arr.length; i++) {
costs[i] = arr[0][i];
if (costs[i] != Integer.MAX_VALUE) {
path[i] = 0;
} else {
path[i] = Integer.MAX_VALUE;
}
}
isCompleted[0] = true;
// 节点0的前驱节点是0
path[0] = 0;
for (int k = 1; k < arr.length; k++) {
// 找到以当前节点为起点的,到达其他节点距离最短的节点
int minIndex = -1;
int min = MAX;
for (int j = 0; j < arr.length; j++) {
if (!isCompleted[j] && costs[j] < min) {
min = costs[j];
minIndex = j;
}
}
if (minIndex == -1) {
continue;
}
// 因为前面的路径是保证了最短路径的,所以遍历获取能到达的最小值显然也是最短路径
isCompleted[minIndex] = true;
for (int i = 1; i < arr.length; i++) {
//动态修改临时权值和路径
if (!isCompleted[i] && arr[minIndex][i] != MAX) {
int value = arr[minIndex][i] + min;
if (value < costs[i]) {
//更新权值
costs[i] = value;
//保存前驱
path[i] = minIndex;
}
}
}
System.out.print("顶点 v1 到 v" + (minIndex + 1) + " 最短路径为");
for (int i = 0; i < path.length; i++) {
if (i == minIndex) {
System.out.print(" <- " + "v" + (minIndex + 1));
int pre = path[minIndex];
while (pre != 0) {
System.out.print(" <- " + "v" + (pre + 1));
pre = path[pre];
}
}
}
System.out.print("<- v1 权值为" + costs[minIndex] + "\n");
}
}
2、弗洛伊德(Floyd)
思想及原理略。
算法求解过程如图:
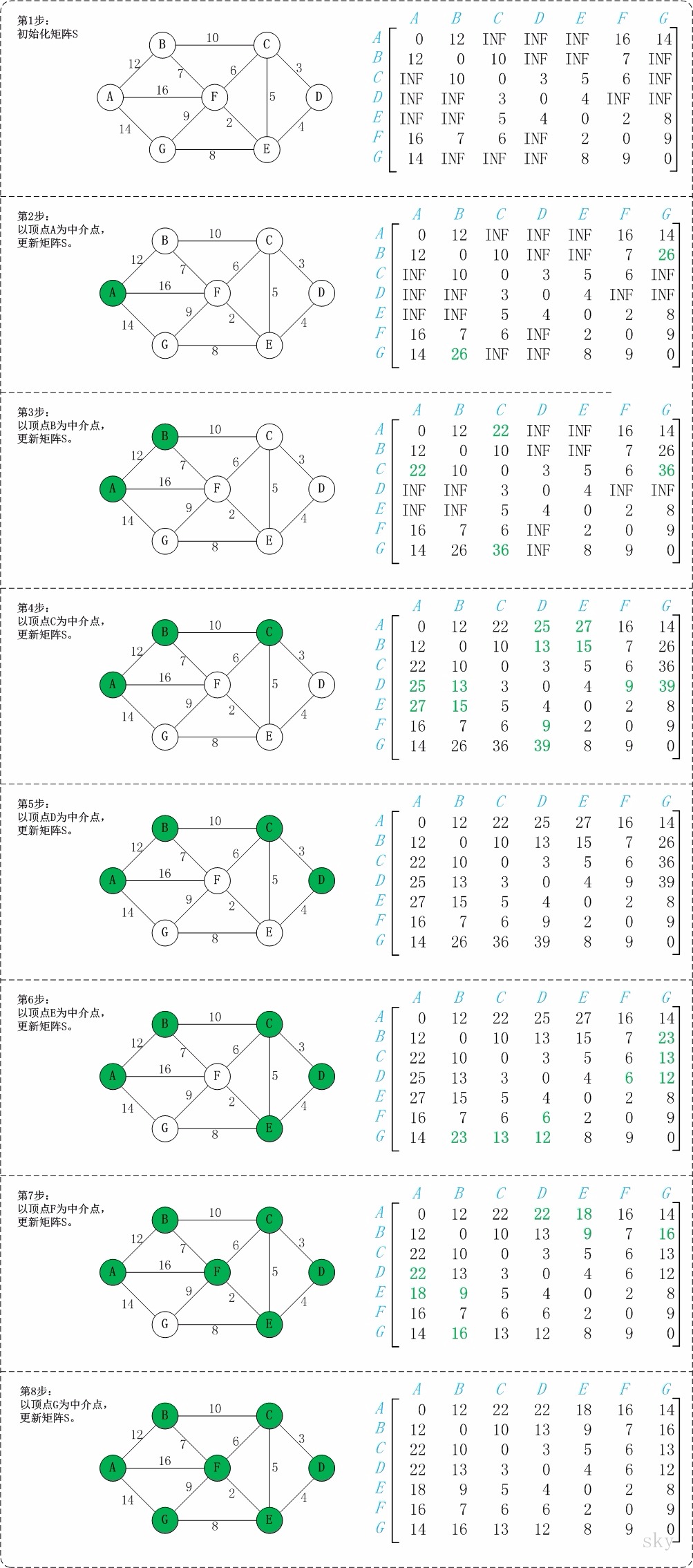
代码实现:
public void floyd() {
System.out.println("Floyd算法 :");
int[][] arr = new int[adjMatrix.length][adjMatrix.length];
//p[0][1] = 3表示节点0到节点1的最短路径经过了3,即0->3->1
int[][] path = new int[arr.length][arr.length];
//初始化path,初始状态path[i][j] =j,表示i直接到j不经过其他点
//此时graph保存的也是i直接到j的路径长度,MAX表示此路不通
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length; j++) {
arr[i][j] = adjMatrix[i][j];
path[i][j] = j;
}
}
for (int i = 0; i < arr.length; i++) {
for (int x = 0; x < arr.length; x++) {
for (int y = 0; y < arr.length; y++) {
if (arr[x][i] == MAX || arr[i][y] == MAX || x == y) {
continue;
}
//如果以i的路过点的路径比当前所存储的最短路径短的话
//则更新此路径为最短路径,并在path中标注出当前最短路径是经过i达到的
if (arr[x][y] > arr[x][i] + arr[i][y]) {
arr[x][y] = arr[x][i] + arr[i][y];
path[x][y] = i;
}
}
}
}
for (int i = 0; i < arr.length; i++) {
for (int j = i + 1; j < arr.length; j++) {
int k = path[i][j];
System.out.print("(" + i + "," + j + ")" + arr[i][j] + ": ");
System.out.print(i);
while (k != j) {
System.out.print("->" + k);
k = path[k][j];
}
System.out.print("->" + j + " ");
}
System.out.println();
}
}
五、测试数据
1、测试数据1
private static void testData1() {
Vertex<String> v1 = new Vertex<>("v1");
Vertex<String> v2 = new Vertex<>("v2");
Vertex<String> v3 = new Vertex<>("v3");
Vertex<String> v4 = new Vertex<>("v4");
Vertex<String> v5 = new Vertex<>("v5");
Vertex<String> v6 = new Vertex<>("v6");
Vertex[] vertices = new Vertex[]{v1, v2, v3, v4, v5, v6};
Edge e1 = new Edge(v1, v2, 5);
Edge e2 = new Edge(v1, v3, 7);
Edge e3 = new Edge(v1, v4, 4);
Edge e4 = new Edge(v1, v6, 8);
Edge e5 = new Edge(v2, v3, 9);
Edge e6 = new Edge(v3, v4, 5);
Edge e7 = new Edge(v3, v6, 6);
Edge e8 = new Edge(v4, v5, 5);
Edge e9 = new Edge(v4, v6, 3);
Edge e10 = new Edge(v5, v6, 1);
Edge[] edges = new Edge[]{e10, e2, e3, e4, e5, e6, e7, e8, e9, e1};
Graph graph = new Graph(vertices, edges, GraphType.Undigraph);
graph.printGraph();
graph.depthFirstSearch();
System.out.println();
graph.breadthFirstSearch();
System.out.println();
graph.prim();
graph.kruskal();
}
输出结果
0 5 7 4 0 8
5 0 9 0 0 0
7 9 0 5 0 6
4 0 5 0 5 3
0 0 0 5 0 1
8 0 6 3 1 0
深度优先遍历: v1 -> v2 -> v3 -> v4 -> v5 -> v6 ->
广度优先遍历: v1(4) -> v2(3) -> v3(2) -> v4(2) -> v6(1) -> v5(0) ->
Prim算法:
最小生成树边有顶点 v1到顶点 v4 ,权值为 4
最小生成树边有顶点 v4到顶点 v6 ,权值为 3
最小生成树边有顶点 v6到顶点 v5 ,权值为 1
最小生成树边有顶点 v1到顶点 v2 ,权值为 5
最小生成树边有顶点 v4到顶点 v3 ,权值为 5
该图最小生成树的权最小值为: 18
Kruskal算法:
最小生成树边有顶点 v5 到定点 v6 权值为 1
最小生成树边有顶点 v4 到定点 v6 权值为 3
最小生成树边有顶点 v1 到定点 v4 权值为 4
最小生成树边有顶点 v3 到定点 v4 权值为 5
最小生成树边有顶点 v1 到定点 v2 权值为 5
该图最小生成树的权最小值为: 18
2、测试数据2
public static void testData2() {
Vertex<String> v1 = new Vertex<>("v1");
Vertex<String> v2 = new Vertex<>("v2");
Vertex<String> v3 = new Vertex<>("v3");
Vertex<String> v4 = new Vertex<>("v4");
Vertex<String> v5 = new Vertex<>("v5");
Vertex<String> v6 = new Vertex<>("v6");
Vertex[] vertices = new Vertex[]{v1, v2, v3, v4, v5, v6};
Edge e1 = new Edge(v1, v2, 6);
Edge e2 = new Edge(v1, v3, 1);
Edge e3 = new Edge(v1, v4, 5);
Edge e4 = new Edge(v2, v3, 5);
Edge e5 = new Edge(v2, v5, 3);
Edge e6 = new Edge(v3, v4, 5);
Edge e7 = new Edge(v3, v5, 6);
Edge e8 = new Edge(v3, v6, 4);
Edge e10 = new Edge(v4, v6, 2);
Edge e9 = new Edge(v5, v6, 6);
Edge[] edges = new Edge[]{e2, e3, e4, e5, e6, e7, e8, e9, e1, e10};
Graph graph = new Graph(vertices, edges, GraphType.Undigraph);
graph.printGraph();
graph.depthFirstSearch();
System.out.println();
graph.breadthFirstSearch();
System.out.println();
graph.prim();
graph.kruskal();
}
输出结果
0 6 1 5 0 0
6 0 5 0 3 0
1 5 0 5 6 4
5 0 5 0 0 2
0 3 6 0 0 6
0 0 4 2 6 0
深度优先遍历: v1 -> v2 -> v3 -> v4 -> v6 -> v5 ->
广度优先遍历: v1(3) -> v2(3) -> v3(3) -> v4(2) -> v5(1) -> v6(0) ->
Prim算法:
最小生成树边有顶点 v1到顶点 v3 ,权值为 1
最小生成树边有顶点 v3到顶点 v6 ,权值为 4
最小生成树边有顶点 v6到顶点 v4 ,权值为 2
最小生成树边有顶点 v3到顶点 v2 ,权值为 5
最小生成树边有顶点 v2到顶点 v5 ,权值为 3
该图最小生成树的权最小值为: 15
Kruskal算法:
最小生成树边有顶点 v1 到定点 v3 权值为 1
最小生成树边有顶点 v4 到定点 v6 权值为 2
最小生成树边有顶点 v2 到定点 v5 权值为 3
最小生成树边有顶点 v3 到定点 v6 权值为 4
最小生成树边有顶点 v2 到定点 v3 权值为 5
该图最小生成树的权最小值为: 15
3、测试数据3
public static void testData3() {
Vertex<String> a = new Vertex<>("a");
Vertex<String> b = new Vertex<>("b");
Vertex<String> c = new Vertex<>("c");
Vertex<String> d = new Vertex<>("d");
Vertex<String> e = new Vertex<>("e");
Vertex[] vertices = new Vertex[]{a, b, c, d, e};
Edge e1 = new Edge(a, b, 3);
Edge e2 = new Edge(a, d, 7);
Edge e3 = new Edge(b, c, 4);
Edge e4 = new Edge(b, d, 2);
Edge e5 = new Edge(c, d, 5);
Edge e6 = new Edge(c, e, 6);
Edge e7 = new Edge(d, e, 4);
Edge[] edges = new Edge[]{e1, e2, e3, e4, e5, e6, e7};
Graph graph = new Graph(vertices, edges, GraphType.Undigraph);
graph.printGraph();
graph.dijkstra();
graph.floyd();
}
输出结果
0 3 0 7 0
3 0 4 2 0
0 4 0 5 6
7 2 5 0 4
0 0 6 4 0
Dijkstra算法:
顶点 v1 到 v2 最短路径为 <- v2<- v1 权值为3
顶点 v1 到 v4 最短路径为 <- v4 <- v2<- v1 权值为5
顶点 v1 到 v3 最短路径为 <- v3 <- v2<- v1 权值为7
顶点 v1 到 v5 最短路径为 <- v5 <- v4 <- v2<- v1 权值为9
Floyd算法 :
(0,1)3: 0->1 (0,2)7: 0->1->2 (0,3)5: 0->1->3 (0,4)9: 0->3->4
(1,2)4: 1->2 (1,3)2: 1->3 (1,4)6: 1->3->4
(2,3)5: 2->3 (2,4)6: 2->4
(3,4)4: 3->4
总访问次数: 97次, 一般般帅 创建于 2017-03-28, 最后更新于 2020-06-25
 欢迎关注微信公众号,第一时间掌握最新动态!
欢迎关注微信公众号,第一时间掌握最新动态!